|
Author
|
Topic: JI tuning.. What is it?
|
ed packard
Member From: Show Low AZ
|
 posted 20 September 2003 12:56 PM
profile
posted 20 September 2003 12:56 PM
profile
CD asked for no "what or why" answers to his thread re JI, just "how". No definition was given for what was to be considered JI for his purpose. In this thread, if you are so inclined, please say why you think that what you tuned to is JI or not, and why you like it as a tuning. Feel free to use words and/or numbers to describe/justify your system/tuning. |
Karlis Abolins
Member From: Burien, WA, USA
|
 posted 20 September 2003 01:06 PM
profile
posted 20 September 2003 01:06 PM
profile
My take on JI is sound. On my E9, I tune the E's to 0 cents. I then tune the G# and B so that when I strum, It makes that "BIG" major harmony across all 1-3-5's. Then I pedal A and B and do the same thing. I then tune the BC for a "BIG" minor harmony. Same for the other pedals. JI to me is making the major and minor chords sound "sweet".Karlis |
Bobby Lee
Sysop From: Cloverdale, North California, USA
|
 posted 20 September 2003 02:10 PM
profile
posted 20 September 2003 02:10 PM
profile
Just Intonation is the tuning system of pure harmonies, where the each interval can be expressed as a ratio of two frequencies. For example, if A is 440 Hz, the E above it is 440 x 3/2, or 660 Hz.
The ratios used in the E9th tuning are given on a chart I made a few years ago:
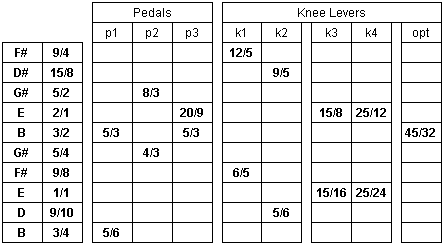
Note that some players pull the F# to 10/9 with pedals down, to harmonize better with the 5/3 of the C# note.
Just intonation is the lack of temperament. Steel players often think of JI as "tempered tuning", because each note falls at a different place on the tuning meter. In truth, the meter's scale is tempered to a system called "equal temperament". Tuning to the correct offsets is necessary if you want to "untemper" your tuning to get the pure harmonies of JI.
I suggest that we start calling JI the "untempered tuning".  ------------------
 Bobby Lee - email: quasar@b0b.com - gigs - CDs, Open Hearts Bobby Lee - email: quasar@b0b.com - gigs - CDs, Open Hearts
Sierra Session 12 (E9), Williams 400X (Emaj9, D6), Sierra Olympic 12 (C6add9),
Sierra Laptop 8 (D13), Fender Stringmaster (E13, A6),
Roland Handsonic, Line 6 Variax |
ed packard
Member From: Show Low AZ
|
 posted 21 September 2003 09:37 AM
profile
posted 21 September 2003 09:37 AM
profile
Kenny; Getting it all to sound "good/sweet" is the whole deal, ..how one gets there is worth defining. I don't know if what you are doing is JI or not. Tuning your E straight up makes your A a bit flat re A=440, ..do you just adjust the A with p1p2 down, or do you adjust the 3rds,5ths, etc. in A also?b0b;
Nice piece of workIt may be a JI example, but to what definition of JI was it aimed? "Lack of temper" pushed to the limit is absence of temper, .. I don't know how to do that, so I must choose my intervals. I vote for, 5ths & 3rds first, and then 7/b7/bb7, next. The term "pure harmonies" in the absolute sense are most closely approached in a system where there are only sine waves, ..in any other system the term "pure" becomes relative: Then we ask, which harmonies will we sacrifice to get the good sound(s) (see Kenny's response). I have taken your chart and played some games with it by calculating the frequencies that it yields and filling in the unspecified notes/intervals. The frequencies yielded are compared with the ET frequencies using the frequency given by tuning string 8 "straight up" on a tuner as the root frequency for the key of E. The assumption here is that we are talking about the common tuner in which the tuning scale is ET based on A=440.
I II III IV V VI VII
III*R 2^(1/12) V-VI
STR/CHG NOTE RATIOS INT(E) b0b(E) Hz ET(E) Hz b0b-ET
K1 G 12/5 b3 395.54 391.99 3.56
1 F# 9/4 2 370.82 369.99 0.84
2 D# 15/8 7 309.02 311.12 -2.10
K2 D 9/5 b7 296.66 293.66 3.00
P2 A 8/3 4 439.49 439.99 -0.50
3 G# 5/2 3 412.03 415.30 -3.27
FILL G 12/5 b3 395.54 391.99 3.56
P3 F# 20/9 2 366.24 369.99 -3.74
K4 F 25/12 b2 343.35 349.22 -5.87
4 E 2/1 OCT 329.62 329.62 0.00
K3 Eb/D# 15/8 7 309.02 311.12 -2.10
FILL D 9/5 b7 296.66 293.66 3.00
P1,P3 C# 5/3 6 274.68 277.18 -2.49
FILL C 8/5 #5 263.70 261.62 2.08
5 B 3/2 5 247.22 246.94 0.28
OPT A#/Bb 45/32 b5 231.76 233.08 -1.31
P2 A 4/3 4 219.75 219.99 -0.25
6 G# 5/4 3 206.01 207.65 -1.64
K1 G 6/5 b3 197.77 195.99 1.78
7 F# 9/8 2 185.41 184.99 0.42
K4 F 25/24 b2 171.68 174.61 -2.93
8 E 1/1 R 164.81 164.81 0.00
K3 Eb/D# 15/16 7 154.51 155.74 -1.23
9 D 9/10 b7 148.33 147.00 1.33
P1 C# 5/6 6 137.34 138.75 -1.41
FILL C 8/10 #5 131.85 130.96 0.89
10 B 3/4 5 123.61 123.61 0.00
CONCLUSIONS:
The key that we hav come closest to justifying is E, or whatever note is on string 8 in this tuning structure. Using any other string than 8 or 4(without changes)as chord root changes the harmonic relationship (ratios) of the intervals for that chord. Using any other notes than those found on strings 8 & 4 (present or implied) as the root of a chord changes the relationship ratios of the intervals found within that chord. If this "tuneup" is played with a group tuned to A=440 and ET, you will be out per col'm VII (beats). If string 8 (the root of the tuning) had been tuned "straight up" re A=441 or higher, there would be fewer flatted intervals re the band/group. Being a bit sharp seems to be accepted, being flat is not. If one does not like beats between the band instruments, this implementation of the tuning does not solve the problem, even in the root key. The instrument(s) have to dwell on the note/harmony long enough for the beats to be noticed (perhaps the principles of Shannons law applies here). Unless one is dealing with sine waves, or only even harmonics, the 3rds (and other intervals)present in each string will still be problematical. Because the 5ths are the third harmonic(h3), and the 3rds are the fifth harmonic(h5)the effect of the "in stringt" thirds may be reduced by reducing the treble response, ..Nashville & Bakersfield don't like that, ..Jerry Byrd does. QUESTIONS:
Is the above "THE" example of JI for the Key of E (or the note on string 8), or is it just one of the possible examples of JI for the Key of E or string 8 note chosen? Can one get to JI by tuning the beats out? Is reducing the beats meor important than not being flat? Is JI a Class of tunings or a single tuning, ..does it include or exclude other tunings. The tuning discussions seem to lean toward, if it is not ET it must be JI, ..and if not ET then it is "tune the beats out". [This message was edited by ed packard on 21 September 2003 at 10:28 AM.]
|
Rick Aiello
Member From: Berryville, VA USA
|
 posted 21 September 2003 11:51 AM
profile
posted 21 September 2003 11:51 AM
profile
Just Intonation: Two Definitions------------------

www.horseshoemagnets.com |
David Doggett
Member From: Philadelphia, Pennsylvania, USA
|
 posted 21 September 2003 12:43 PM
profile
posted 21 September 2003 12:43 PM
profile
Guys, this thread is really getting to the meat of tuning problems. By converting b0b's JI ratio copedent into Hz values around 440 I was able to look into a bunch of questions I have had. Mainly, does JI mean to play every note according to the JI tuned scale, the way a JI tuned keyboard would do, or does it mean to play triads according to a JI triad, the way a steel played with a bar will do? For some chords its about the same either way (I, IV, V, VIm). For other chords (II, IIm) it is not at all the same.I'm pasting in here some of my findings on this from over on Bill Hanky's thread on tuning.
I took b0b's chart of the JI interval ratios for standard E9 tuning and converted the ratios to cents, then to the difference between JI cents and ET cents, then to the Hz A=440 numbers you would tune to on a chromatic tuner. For example, if the E's are tuned 440, then the 3rd (G#) would be 5/4, which would be 13.7 cents flat of ET, or 436.6 Hz, say 437.
The main point here is that a JI major chord triad (I, III, V) should be 440, 437, 440; and a JI minor chord (I, IIIb, V; or VI, I, III) should be 440, 444, 440. But a strict JI scale doesn't give triads like that with some roots (example II, IV#, VI). For that reason, and because of cabinet drop, as b0b and Bill suggested, it would not be a great idea to tune exactly by the strict JI scale. Ignoring cabinet drop, some things work out nicely and others don't. The EG#B triad is 440, 437, 440, exactly as a JI major triad should be. With the A&B pedals down, with no cabinet drop the AC#E triad is 440, 436, 440. One Hz is 0.25 cents, so this is off from JI by only 4 cents, and few people can hear less than 5 cents off. So if you tune your A&B pedals by ear to this chord with the E as the reference (as I do), this triad will be fine with the bar. But the whole triad will be flat at the nut to the extent of your cabinet drop (which flats your reference E's). If you tune the A with the pedal down to 440, and tune the E's JI to that, your E chord at the nut will be sharp to the extent of your cabinet drop. Thus, cabinet drop will only be a problem at the nut, and with the bar your ear will compensate for cabinet drop (provided it's not made out of tin). If you try to tune both triads ET 440, The E's will be off in one triad or the other, to the extent of cabinet drop. And it will be off both with the bar and at the nut. The A pedal + F lever combination will not work at all with this JI tuning. The C#FG# triad will be 436, 443, 437 at the nut (ignoring cabinet drop). With the bar, if you adjust the root to 440 (say to match your bass player - he is tuned ET to 440 isn't he?), the triad will be about 440, 447, 441. The 3rd is 10 Hz sharp from JI, or 40 cents. Youch! However, if you forget the chart and tune the F lever stops by ear to either of the other two strings in the triad, you can get a good JI 440, 437, 441 for this triad. Your F lever will be off outside of this triad, but how often do you use the F lever for anything else? By itself it is good for an augmented chord. But a little disonance is all part of that sound. I tune my 1st and 2nd strings with the 5th string as the root of a B chord. This triad, BD#F#, is 440, 437, 441, by b0b's JI ratio chart, which is about what you will get if you tune this JI by ear with the 5th string as the reference. There is one mystery this chart taught me something about. I was wondering, if you tune your open tonic chord (E) JI, what happens if you move the bar up two frets to play a II chord. Is that the same notes you would get from the JI scale (that is from playing the piano notes on a piano tuned JI to the E scale)? The answer is no. The JI E scale by the ratios says that F#A#C# (II, IV#, VI), should be 441, 438, 436. The 3rd of that chord is very close to a JI 3rd, but that 5th is off by 4 Hz or 16 cents from what we expect of a major 5th. This is because, compared to ET, the VI of the JI scale is flat, like the III is. Playing the II chord with the bar gives 440, 437, 440, if your tonic is tuned JI (if you just move the bar up two frets, your ear will put the root of this II chord at 440 if your bass player and other guitars are tuned ET A=440). Now I don't know which one of those chords we should be aiming for. Does JI mean you keep JI within the chord you are playing, or with the JI scale of the key you are playing in? I'm thinking I'd rather play the triads JI, and forget about the JI scale. Here are some other triads you get with b0b's JI ratio copedent. The relative minor chord (C#minor): 436, 440, 437. That's not bad, using the bar you'd probably hit 440, 444, 441 (a JI minor triad should be 440, 444, 440). The II minor (F#, A, C#, or what you get with the B&C pedals with the 7th string as the root): 441, 440, 436. For this chord you have to keep the A at 440, because it's pegged to the tuner, and is the root of a IV chord we already decided was good. So the solution is to tune the 7th string and C pedal to give 437, 440, 437 (and also 437 on the 4th string). If there is a little dissonance when you use the 7th string as the 9th in a chord or as II in a scale, it will probably be passable. What all this says is that if you just tune your strings and pedals to give sweet sounding (or minimum beats) major and minor chords for the main chords in the key you tune in (E typically), things will work out better than if you tried to tune everything rigorously to a JI scale. This tells me something very interesting. The pedal steel doesn't handle JI tuning like a JI tuned keyboard does. You can't play a sweet II chord on a JI tuned keyboard, but you can on a pedal steel. With the bar, you don't keep JI with the scale of the key, but you do keep JI with the root of the chord, which in many cases may be better. In other words, the steel can not only keep JI when modulating to another key, it can play JI chords within the same key in ways a keyboard or fretted instrument cannot. Is this a great instrument, or what?!  When I get a chance I will post b0b's JI ratio copedent converted to Hz at A=440. I'll also post a revised JI copedent that gives precedent to the main triads, as described above. My home computer's lost its internet connection because of a virus or something. So this coud take awhile. [This message was edited by David Doggett on 29 September 2003 at 09:46 AM.]
|
Bengt Erlandsen
Member From: Brekstad, NORWAY
|
 posted 21 September 2003 12:51 PM
profile
posted 21 September 2003 12:51 PM
profile
When tuning to JI how do one deal with that the fretboard is marked ET??Bengt Erlandsen |
Bobby Lee
Sysop From: Cloverdale, North California, USA
|
 posted 21 September 2003 01:06 PM
profile
posted 21 September 2003 01:06 PM
profile
I recommend Harry Partch's classic book Genesis of a Music to anyone who wants to understand the definition of JI. There are many charts in it that show the width of the various JI intervals in cents.
My E9th chart only shows the intervals that steel guitarists try to tune to - the ones that are close to the 12-tone system of music. Partch identifies other intervals that are not as frequently heard. The 11/9, for example, is 347 cents wide. That's 47 cents sharp of the ET minor third. You hear it in blues sometimes, but it is not part of our 12-tone music system.
Click here for Partch's famous "One-Footed Bride" diagram.------------------
 Bobby Lee - email: quasar@b0b.com - gigs - CDs, Open Hearts Bobby Lee - email: quasar@b0b.com - gigs - CDs, Open Hearts
Sierra Session 12 (E9), Williams 400X (Emaj9, D6), Sierra Olympic 12 (C6add9),
Sierra Laptop 8 (D13), Fender Stringmaster (E13, A6),
Roland Handsonic, Line 6 Variax |
Bobby Lee
Sysop From: Cloverdale, North California, USA
|
 posted 21 September 2003 01:29 PM
profile
posted 21 September 2003 01:29 PM
profile
Ed's questions:- Can one get to JI by tuning the beats out? JI is by definition beatless.
- Is reducing the beats more important than not being flat? JI major thirds don't sound flat. They sound in tune. But if you go to an interval slightly narrower than the JI major third, it will sound flat. Myself, I'd usually rather have a slow beat happening than risk sounding flat.
- Is JI a Class of tunings or a single tuning, ..does it include or exclude other tunings. I would say that it is a class of tunings, because the actual tuning depends on the starting point. In your calculations, you pinned E at 329.62 Hz. I would have pinned it at 330 Hz (at least) so that A would be 440 Hz. So we already have two different tunings that are both JI.
- The tuning discussions seem to lean toward, if it is not ET it must be JI, ..and if not ET then it is "tune the beats out". Right, and yet many of us use other temperaments. On pedal steel, I tune my thirds 10 cents flat, and the only beatless intervals are the 4ths and 5ths. I do tend to tune my non-pedal steels to JI, though.
------------------
 Bobby Lee - email: quasar@b0b.com - gigs - CDs, Open Hearts Bobby Lee - email: quasar@b0b.com - gigs - CDs, Open Hearts
Sierra Session 12 (E9), Williams 400X (Emaj9, D6), Sierra Olympic 12 (C6add9),
Sierra Laptop 8 (D13), Fender Stringmaster (E13, A6),
Roland Handsonic, Line 6 Variax |
ed packard
Member From: Show Low AZ
|
 posted 21 September 2003 01:29 PM
profile
posted 21 September 2003 01:29 PM
profile
Just to add some more spice, ..you can adjust the "between the strings" intervalic ratios, but you can NOT adjust the "in the string" intervalic ratios, hence adjusted between the strings adjusted 3rds may still clash with in the string unajustable 3rds.Where you pick the string can be used to control the amount of 5th harmonic(h5) = "in the string 3rd". If you pick the string half way between the bar and the bridge you will maximize all "odd" harmonics of the played note(includes the 3rd)and minimize the "even" harmonics. As you pick a bit closer to the bridge the 3rds(h5) tend to decrease while the 5ths(h3) do not decrease as quickly. Harmonic content can be selectively changed by where you pick the string. |
David Doggett
Member From: Philadelphia, Pennsylvania, USA
|
 posted 21 September 2003 01:34 PM
profile
posted 21 September 2003 01:34 PM
profile
Bengt, except when playing very fast, steelers only use the fret marks as a visual guide to get close, with the final pitch being determined by the ears. If you are playing by yourself, your ears will try to make your bar play where it should JI. The difference between JI and the ET frets is almost imperceptible visually.If you are playing with a group, your ears will try to make the bar match the root pitch of the group at any particular musical moment. That will usually be the bass note, but might be a singer or another lead instrument if you are harmonizing with them. The point of the stuff above is that with the bar you can match the root of your chord to the ET pitch of the group, even if your chord intervals are tuned JI, and you will do this pretty much automatically. Only at the nut would your root possibly be off from ET, but not if you tune your E's (or A's) to A=440. This is why many steelers think you don't necessarily need to tune every string and stop ET to play with ET instruments. Nobody ever did before the advent of cheap handheld ET tuners.[This message was edited by David Doggett on 21 September 2003 at 01:35 PM.] |
Bobby Lee
Sysop From: Cloverdale, North California, USA
|
 posted 21 September 2003 01:34 PM
profile
posted 21 September 2003 01:34 PM
profile
Right you are, Ed. The harmonic overtone series inherent in the string's vibration is JI. |
Karlis Abolins
Member From: Burien, WA, USA
|
 posted 21 September 2003 01:35 PM
profile
posted 21 September 2003 01:35 PM
profile
Ed, I start by tuning the E's to 0 cents on my tuner. I don't know the exact frequency but the E's are the starting point for me. I then tune the 3rd's and 5th's so they sound sweet relative to the E's. Next I pedal A and B together. This flats the E's a small amount because of cabinet drop. It is an unimportant detail adjusted for by a slight bar movement (within the vibrato for example). I then tune the A and B pedals relative to the new value of the E's so that it sounds sweet again. Almost all of my pedals are tuned relative to an unchanged string taking into account the slight cabinet drop or raise. For the B and C pedal combination I use the value of the B pedal as the starting point.
I don't know if I am getting "strict" just intonation but the desired sweet sound is my primary goal.Karlis |
ed packard
Member From: Show Low AZ
|
 posted 21 September 2003 03:16 PM
profile
posted 21 September 2003 03:16 PM
profile
b0b:
The "pinning" that I did was to E "straight up" as that is the root of the tuning here discussed, and that is the way that most pickers would tune it. Doing so makes the A not equal to 440 (exact) in the 12th root of two system. Some folk like to use the A=441 setting on the tuner, ..this gets the Es closer.Another thing that should show up from these comments and references (thanks Rick A) is that we have a problem with the meaning of words over time, and across cultures. JI was probably used with respect to the non Chroma notes first (many moons ago), so it majored in "fixing" diatonic major and the diatonic minor scales. I am not sure if we can push the principle to include quarter tone scales, and scales with other than our preferred intervals, ..might have to change the name, ..depends upon what the definition(s) of JI turn(s) out to be. Same thoughts for Peleg, Arabic, Slendro, and other "different" scales. Re "Right you are", ..I'm not sure I said what you think I said. DD; You are having more fun than is legal! Kenny; I'm with you, ..playing with the names and principles is fun, but in the end, I don't care what is called as long as it sounds good in the musical environment of choice; a different kind of communication. |
Bobby Lee
Sysop From: Cloverdale, North California, USA
|
 posted 21 September 2003 03:49 PM
profile
posted 21 September 2003 03:49 PM
profile
JI does not depend on any "definition", Ed. Just intonation is the natural harmony of sound vibrations. It is defined by the laws of physics. The harmonics of a vibrating string at various points along its length are JI.
In contrast, temperaments are mathemetical systems designed to solve the problem of playing in multiple keys on instruments that, unlike a steel guitar, are limited to 12 fixed pitches per octave.
You cannot make a vibrating string produce a tempered overtone. The string will not cooperate. You can't sound a harmonic on a string that isn't a JI interval above the open pitch. JI is physics.
Physics doesn't recognize temperaments. Temperaments rely on the fact that human perception of harmony isn't perfect. We hear things in tune that really aren't in tune. Some of it is cultural conditioning, and some of it is just the limitations of our ears and brains.------------------
 Bobby Lee - email: quasar@b0b.com - gigs - CDs, Open Hearts Bobby Lee - email: quasar@b0b.com - gigs - CDs, Open Hearts
Sierra Session 12 (E9), Williams 400X (Emaj9, D6), Sierra Olympic 12 (C6add9),
Sierra Laptop 8 (D13), Fender Stringmaster (E13, A6),
Roland Handsonic, Line 6 Variax |
ed packard
Member From: Show Low AZ
|
 posted 21 September 2003 04:21 PM
profile
posted 21 September 2003 04:21 PM
profile
Aha b0b, a bit of semantics at issue here; I hold that..A phenomenon does not depend upon the definition, ..the definition is only required to limit the use of the term and facilitate communication about the subject under discussion.Them there "laws of Physics" are suspect at all times. I recall when it was found that the atom was the smallest particle that would ever exist, .they pleaded the "Laws of Physics". I recall when it was said that nothing could be faster than the speed of light, ..they pleaded the "Laws of Physics". The latest that I know of is gravity ala Newton does not hold under certain conditions, ..That would appear on the surface to be against the "Laws of Physics". This is not to say that the Physics of things do or do not change, but that our understanding and descriptions of these things do. Can I that the harmonics in a vibrating string do not have to agree with the common formulae for frequencies as a function of material, dimensions, tensions, etc.? Yes,..so even those are not an absolute constant. Maybe more on the harmonic series later after we see where what has been started above goes. |
Rick Aiello
Member From: Berryville, VA USA
|
 posted 21 September 2003 04:47 PM
profile
posted 21 September 2003 04:47 PM
profile
Inharmonicity ... Physics is Physics  Anyway ... I did a similar chart to y'alls ... years ago when I was first learnin' .... It is the position of the actual JI notes of the C scale ... "relative" to the frets... in a JI C6 tuned steel. (lo to hi ... E G A C E ... sorry for the "non-pedal" tuning) 
5 4 3 2 13(0) 5(0) 6(0) 1(0) 3(0)
4(+12) 5#(+12) 7b(+34) 2b(+12) 4(+12)
5b(+4) 6(-18) 7(+4) 2(+4) 5b(+4)
5(+16) 7b(+16) 1(+16) 3b(+16) 5(+16)
5#(+28) 7(-14) 2b(+28) 3(-14) 5#(+28)
6(-2) 1(-2) 2(+20) 4(-2) 6(-2)
7b(+32) 2b(+10) 3b(+32) 5b(-10) 7b(+32)
7(+2) 2(+2) 3(+2) 5(+2) 7(+2)
1(+14) 3b(+14) 4(+14) 5#(+14) 1(+14)
2b(+26) 3(-16) 5b(+6) 6(-16) 2b(+26)
2(+18) 4(-4) 5(+18) 7b(+18) 2(+18)
3b(+30) 5b(-12) 5#(+30) 7(-12) 3b(+30)
3(0) 5(0) 6(0) 1(0) 3(0) EX: First string ... if you want the JI "F note" in the C scale ... the bar has to be (+)12 cents sharp of fret 1. The open E is already (-)14 cents flat ... the F needs to be (-)2 flat ... so the bar must be placed (+)12 cents sharp of fret 1 to compensate. Just thought it may be of some interest ... [This message was edited by Rick Aiello on 21 September 2003 at 06:07 PM.]
|
ed packard
Member From: Show Low AZ
|
 posted 21 September 2003 05:24 PM
profile
posted 21 September 2003 05:24 PM
profile
Rick;
Nice presentation, and I recognize the reference, ..used to get the journal of the A.S. in those days. Started messing with Spreadsheet/music calcs when there was only Visicalc. Then God bless Lotus! If you did engineering/physics calcs on a spreadsheet you were labeled a nut, ..spreadsheets were just for accountants then.Are you familiar with what happens at MITs Media Lab? |
Rick Aiello
Member From: Berryville, VA USA
|
 posted 21 September 2003 05:58 PM
profile
posted 21 September 2003 05:58 PM
profile
Nope ... |
ed packard
Member From: Show Low AZ
|
 posted 22 September 2003 08:43 AM
profile
posted 22 September 2003 08:43 AM
profile
Many moons ago, when this forum was just getting up and running, when the main content was hello, how are you, I broke my G# last night, I decided to add some more technical "stuff" to the pot. Some of this "stuff" showed up in what is now the Article section of the forum. One piece of "stuff" has to do with Music & science. It covers the harmonic series of the vibrating string and compares a "string harmonics based scale with a "constant ratio" based scale. The constant ratio based scale shown is what is usually called ET or equal temperament and is based upon the 12th root of 2,=2^(1/12)=1.0595xxx. There were some "goofs" in my blurb that I noticed after it was put up, but I decided to see if anyone would catch them, ..5 or 6 years and no one has complained, ..try your hand at it.Some time later b0b added an article to this section that deals with Just Intonation, the chart from which is found above in b0b's post. There is a good reference in his article to a web site re Just Intonation.
I was starting to do up some more charts for this thread, and decided that they would be essentially about like those in the blurb, so see the blurb if you are interested.
b0b takes the more musically conventional approach of giving the ratios a simple fractions, ..I prefer to give them as decimal values, ..2/3 = 1.500000 etc., ..the conversion is not difficult. My article has several points to make re tuning, beats, scales, Intervals, neck layout, string tension, and two octave seven tone chord structure all being related as decendants of the nature of string vibration. One curve in the article that might throw some folk is that I "normalized" the frequencies involved to 1, ..this convenience makes the decimal ratios the same as the frequency values if the ref frequency of the scale = 1 Hz resulting in easier to make tables for b0b who did the HTML to put the article on the site. Some folk calculate cents by taking a frequency value and dividing it by 100, ..close but no cigar. The 12 tone octave in ET uses the 12th root of 2 to obtain its "constant ratio" for halftones, ..for cents it would be the 1200th root of 2 to get to cents. |
ed packard
Member From: Show Low AZ
|
 posted 22 September 2003 12:49 PM
profile
posted 22 September 2003 12:49 PM
profile
Ed's questions, b0b's answers, Ed's comments[Can one get to JI by tuning the beats out?] (JI is by definition beatless.)
Then the fractions /ratios that were given for JI are only close. If decimals for the actual frequency ratios were used (not conveniently simplified fractions)there would be no beats. [Is reducing the beats more important than not being flat?]
( JI major thirds don't sound flat. They sound in tune. But if you go to an interval slightly narrower than the JI major third, it will sound flat. Myself, I'd usually rather have a slow beat happening than risk sounding flat.)
A matter of taste and preference, enjoy. [Is JI a Class of tunings or a single tuning, ..does it include or exclude other tunings.]
(I would say that it is a class of tunings, because the actual tuning depends on the starting point. In your calculations, you pinned E at 329.62 Hz. I would have pinned it at 330 Hz (at least) so that A would be 440 Hz. So we already have two different tunings that are both JI.)
Sorry for some confusion, ..by class I did not mean simply moving the frequency base (329.62, 330, or?, but would it also include some other named "temperaments" like Barnes-Bach etc.. In subsequent discourse it has been mentioned that you like NON tempered (or similar) as a functional description/name of JI, therein lies the answer. [the tuning discussions seem to lean toward, if it is not ET it must be JI, ..and if not ET then it is "tune the beats out".]
(Right, and yet many of us use other temperaments. On pedal steel, I tune my thirds 10 cents flat, and the only beatless intervals are the 4ths and 5ths. I do tend to tune my non-pedal steels to JI, though.)
concurrence indeed, ..if JI is a singular tuning structure (not a class), and is beatless re the given frequencies, then there are many other ways to tune than ET and JI, and most pickers have their own preferences and might as well name it after themselves. Back to "right you are" and my answer to b0b, ..As long as we agree that zero beats exist between JI and the Harmonic series derived scales(as opposed to the fractional ratios given from which the JI frequencies were calculated), then I accept the "right you are" comment, and JI becomes the tuning structure identified with an harmonic series derived scale. So what do the rest of you guys and gals call your tuning method? [This message was edited by ed packard on 22 September 2003 at 01:29 PM.] |
Bobby Lee
Sysop From: Cloverdale, North California, USA
|
 posted 22 September 2003 04:12 PM
profile
posted 22 September 2003 04:12 PM
profile
We're very close on this, Ed, but I have to disagree with you on one point: quote:
[Can one get to JI by tuning the beats out?] (JI is by definition beatless.)
Then the fractions /ratios that were given for JI are only close. If decimals for the actual frequency ratios were used (not conveniently simplified fractions)there would be no beats.
The fractions are not "conveniently simplified" - they are the actual ratios of the frequencies. You can approximate 4/3 to 1.33333333, but in a JI system the actual frequency of A is the frequency of E times 4 divided by 3.
To me, the ratios are a clearer indication of what is actually going on. You can't tell by looking at a decimal multipliers if notes will harmonize or not. If the ratios are small whole numbers, harmony is guaranteed by the "laws of physics".------------------
 Bobby Lee - email: quasar@b0b.com - gigs - CDs, Open Hearts Bobby Lee - email: quasar@b0b.com - gigs - CDs, Open Hearts
Sierra Session 12 (E9), Williams 400X (Emaj9, D6), Sierra Olympic 12 (C6add9),
Sierra Laptop 8 (D13), Fender Stringmaster (E13, A6),
Roland Handsonic, Line 6 Variax |
Bobby Lee
Sysop From: Cloverdale, North California, USA
|
 posted 22 September 2003 04:15 PM
profile
posted 22 September 2003 04:15 PM
profile
As for my own tuning method, I call it "b0b's temperament".  |
ed packard
Member From: Show Low AZ
|
 posted 23 September 2003 09:03 AM
profile
posted 23 September 2003 09:03 AM
profile
Good name (b0b's temperament), so for the next charts I will shorten it to b0b's JI to make shorter col'm headings.Some may be interested in how the h (harmonic) series is derived. The next chart will illustrate this. It will also show that the "small number" fractions used in the books to "define" JI are not the real ratios for the h series. It will also be seen that the real ratios given as decimals need only 4 decimal places before turning to zeros. The basis of the h series (JI?) is to take a root frequency, multiply it be sucessive integers (starting with 1). These sucessive intergers become h1, h2, h3 etc. We shall carry this up to h32 to illustrate the forming of the diatonic, chromatic, and the beginnings of the quarter tone scales. After multiplying the chosen root frequency by the sucessive integers to get the hn frequencies, we then divide these hn frequencies by a series of binary numbers (1,2,4,8,16 etc.) to get the frequencies of the intervals for the h(JI?) scale. It is interesting to note that the binary numbers advance by binary grouping also ( 2 2s, 4 4s, 8 8s, 16 16s). Now that we have the root frequency and the interval's frequencies, we make a fraction of these two (interval freq/root freq) and this is the RATIO we want. These fractions are large and cumbersome to work with, so we can try reducing them to their smallest form for convenience only to find that they are still unweildy. We now have a choice to make, ..either simplify (approximate) the ratio with a non accurate but close fraction, or convert the original fraction (freq/freq) to decimal form. If we convert the freq/freq fration to decimal form, it will be noticed that none of the decimal places (after the dec point)need exceed 4, and that all the numbers before the dec point are 1 until we get to the octave. These are the "beatless" ratios, the simplified (substituted) fractions are not. For the purpose of the chart, A has been "pinned" to 440 Hz and let the rest fall per the h series giving a C=270.769 Hz. The scale solved for is Root = C = 270.769 Hz. CALCULATING THE h SERIES RATIOS:
I II III IV V VI VII
(hn/m Hz)/(h1Hz) =
hn hn Hz hn/m Hz m INT Note, C h RATIO
32 8664.61 541.538 16 OCT C 2.00000
31 8393.84 524.615 16 1.93750
30 8123.07 507.692 16 7 B 1.87500
29 7852.30 490.769 16 1.81250
28 7581.53 473.846 16 b7 Bb 1.75000
27 7310.76 456.923 16 1.68750
26 7039.99 440.000 16 6 A 1.62500
25 6769.23 423.077 16 #5 G#-Ab 1.56250
24 6498.46 406.154 16 5 G 1.50000
23 6227.69 389.230 16 b5 F#-Gb 1.43750
22 5956.92 372.307 16 4 F 1.37500
21 5686.15 355.384 16 1.31250
20 5415.38 338.461 16 3 E 1.25000
19 5144.61 321.538 16 b3 D#-Eb 1.18750
18 4873.84 304.615 16 2 D 1.12500
17 4603.07 287.692 16 b2 C#-Db 1.06250
16 4332.30 541.538 8 OCT C 2.00000
15 4061.54 507.692 8 7 B 1.87500
14 3790.77 473.846 8 b7 Bb 1.75000
13 3520.00 440.000 8 6 A 1.62500
12 3249.23 406.154 8 5 G 1.50000
11 2978.46 372.307 8 4 F 1.37500
10 2707.69 338.461 8 3 E 1.25000
9 2436.92 304.615 8 2 D 1.12500
8 2166.15 541.538 4 OCT C 2.00000
7 1895.38 473.846 4 b7 Bb 1.75000
6 1624.61 406.154 4 5 G 1.50000
5 1353.85 338.461 4 3 E 1.25000
4 1083.08 541.538 2 OCT C 2.00000
3 812.31 406.154 2 5 G 1.50000
2 541.54 541.538 1 OCT C 2.00000
1 270.77 270.769 1 R C 1.00000
[This message was edited by ed packard on 23 September 2003 at 05:57 PM.] |
Bobby Lee
Sysop From: Cloverdale, North California, USA
|
 posted 23 September 2003 04:46 PM
profile
posted 23 September 2003 04:46 PM
profile
I don't know what that is, Ed, but it ain't just intonation. If A is 440 Hz, how can E be 338.461? That interval won't sound remotely in tune. In JI, the third and the sixth sound sweet together.
I suppose I should eat some crow here. It's obvious from these calculations that the harmonic series doesn't give you all of the notes of the JI scale. To get the sixth interval in JI, for example, you need to multiply the fundamental by 5/3 (1.666...). This is very different from the 1.625 mutiplier that Ed used.
Clearly, the harmonic overtone series and just intonation are two different things. I stand corrected.------------------
 Bobby Lee - email: quasar@b0b.com - gigs - CDs, Open Hearts Bobby Lee - email: quasar@b0b.com - gigs - CDs, Open Hearts
Sierra Session 12 (E9), Williams 400X (Emaj9, D6), Sierra Olympic 12 (C6add9),
Sierra Laptop 8 (D13), Fender Stringmaster (E13, A6),
Roland Handsonic, Line 6 Variax |
Rick Aiello
Member From: Berryville, VA USA
|
 posted 23 September 2003 06:10 PM
profile
posted 23 September 2003 06:10 PM
profile
13/8 is the overtone (harmonic) 6th .... 5/3 is the 5-limit JI 6th ... Here is a nice paper that gives you a Tour up the Harmonic Series... it discusses various aspects of the series and how it relates to the various JI ratios. The Anatomy of an Octave that I posted a few days ago is still the best reference I have seen ... its got "it all"  [This message was edited by Rick Aiello on 23 September 2003 at 06:27 PM.] |
David Doggett
Member From: Philadelphia, Pennsylvania, USA
|
 posted 23 September 2003 06:48 PM
profile
posted 23 September 2003 06:48 PM
profile
Here are the notes of the E9 tuning in JI ratios, JI cents, ET cents, ET-JI difference in cents, and in relation to A=440 Hz. The left column gives the string and pedal/knee combination. The pedals are A,B,C, and the knees are according to the note they give: D, Eb, F, Bb, G.
String Scale JI Cents ET Diff. A=440
3+B A IV 440
3 G# III 437
1+G G 444
1, 4+C F# II 441
4+F F 443
4 E I 2/1 1200.0 1200 0 440
2, 4+Eb D# VII 15/8 1088.3 1100 -12 437
2+D D 9/5 1017.6 1000 18 444
5+A C# VI 5/3 884.4 900 -16 436
C 8/5 813.7 800 14 443
5 B V 3/2 702.0 700 2 440
5+Bb A# 45/32 590.2 600 -10 438
6+B A IV 4/3 498.1 500 -2 440
6 G# III 5/4 386.3 400 -14 437
7+G G 6/5 315.6 300 16 444
7 F# II 9/8 203.9 200 4 441
8+F F 16/15 111.7 100 12 443
8 E I 1/1 0.0 0 0 440
8+Eb D# VII 437
9 D 444
10+A C# VI 436
C 443
10 B V 440
[This message was edited by David Doggett on 29 September 2003 at 10:10 AM.]
|
ed packard
Member From: Show Low AZ
|
 posted 23 September 2003 06:54 PM
profile
posted 23 September 2003 06:54 PM
profile
Forget the crow stuff, ..no good even with salt, I've been there.I may have messed up somewhere, ..check the math. Would not be the first time. The scale solved for was the key of C, ..so (fC+fG)/2 should equal fE; Any difference between the fE from this calculation and the fE from the h series calc would be "beats". I just reran the calc, ..dead on, ..check me. In the common JI approach one uses the fractions as the ratio to determine the frequencies. In the series that I have shown the frequencies are used to determine the ratios. Tomorrow I will post the same type of charts for the derivation of ET, and b0b's JI, ..all based upon the C scale where C=the 270.769 Hz obtained by "pinning" A to 440 Hz via the h series. That might shed some light on the issue. Just Intonation sounds like "Just in One Key" for instruments with fixed string length. For the steel with changeable string length via the bar, any key/fret. For the PSG where any string may become a root it sounds like big trouble.
|
David Doggett
Member From: Philadelphia, Pennsylvania, USA
|
 posted 23 September 2003 07:17 PM
profile
posted 23 September 2003 07:17 PM
profile
The first copedent below is the one b0b posted above in JI ratios, converted to A=440 Hz. Rigorous adherence to this tuning gives major problems with the A pedal + F lever combination, and the IIm obtained with the B+C pedals (see my first post above for what the Hz meter readings would be for these triads).The next copedent is what you get if you: 1) tune the F lever to give a JI sounding major chord referenced to the A pedal and open strings, 2) tune the C pedal and 7th string to a JI sounding minor chord referenced to the A (440) of the B pedal. Both of these copedents assume no cabinet drop. If you want to incorporate cabinet drop, you would have to add or subtract that on certain unpedaled strings. For example, my Fessy gives about 2 Hz (about 8 cents) drop on the E strings when I press the A&B pedals. So if I wanted to peg my B pedal to A=440, I would need to add 2 Hz to the E strings (and any other strings not acted on by the A&B pedals). If I wanted to peg my open E strings ET to A=440, I would need to subtract 2 Hz from the stops of the A&B pedals. If you tune by ear, this all happens automatically. You would only need to make these types of corrections to the below copedents if you wanted to tune completely by the meter readout without listening. I haven't checked out what cabinet drop does with changes other than the A&B pedals. I have a bad feeling that some strings and stops might not handle cabinet drop problems as well as the example above with the A&B pedals. That's a future investigation that I am not looking forward to. Tuning everything ET does not eliminate the cabinet drop problem, and in some cases makes it worse, as I tried to explain in one of my posts above. 
JI scale
F G Bb A B C Eb D
1 F# 441 444
2 D# 437 444
3 G# 437 440
4 E 440 443 441 437
5 B 440 438 436 436
6 G# 437 440
7 F# 441 444
8 E 440 443 437
9 D 444 436
10 B 440 436
JI chords
F G Bb A B C Eb D
1 F# 441 444
2 D# 437 444
3 G# 437 440
4 E 440 432 437 437
5 B 440 438 436 437
6 G# 437 440
7 F# 437 444
8 E 440 432 437
9 D 444 436
10 B 440 436
[This message was edited by David Doggett on 29 September 2003 at 10:14 AM.] |
ed packard
Member From: Show Low AZ
|
 posted 24 September 2003 07:52 AM
profile
posted 24 September 2003 07:52 AM
profile
Rick; Great set of ref's from you. I have scanned the JI ones. Without study, and a quick compare with other "JI" materials, I get the impression that JI is not a constant, or different folks have different views as to what JI is (hence the thread topic in the first place). Do you have an opinion?DD; In your charts, how are you calculating cents in other than ET? If you like you can eliminate the extra editing notices by erasing them each time that you edit, ..took me a while to figure that out. b0b; "I don't know what that is, Ed, but it ain't just intonation." What it is is (read "depends upon what the meaning of is is") the possible harmonic frequencies (h1 thru h32)in a vibrating string that has a fundamental of C=270.769 Hz reduced to single octave frequencies, assuming that all octaves are binarily related (X2, X4, X16, etc.) and same intervals are binarily related also. This ignores the sophistication of disenharmonic issues re string clamping etc. How about for now we call it "natures unrefined vibrating string scale", or I will just use h series as above. OK, deeper into the mud, ..Here is the comparison of the h series, b0bs JI, and ET using C=270.769 Hz as the string root frequency. This value was chosen to force (pin) A to 440 Hz in the h series.
Cref = 270.769 Hz
harmon harmon JI JI ET ET harmon harmon JI
INT C NOTE C RATIOS HZ RATIOS HZ RATIOS HZ -JI HZ -ET HZ -ET HZ
--- --- --- --- --- --- --- --- --- --- ---
OCT C 2.0000 541.538 2/1 541.538 2.0000 541.538 0.000 0.000 0.000
7 B 1.8750 507.692 15/8 507.692 1.8877 511.144 0.000 -3.452 -3.452
b7 A#-Bb 1.7500 473.846 9/5 487.384 1.7818 482.456 -13.538 -8.610 4.929
6 A 1.6250 440.000 5/3 451.282 1.6818 455.377 -11.282 -15.378 -4.096
#5 G#-Ab 1.5625 423.077 8/5 433.230 1.5874 429.819 -10.154 -6.742 3.411
5 G 1.5000 406.154 3/2 406.154 1.4983 405.695 0.000 0.458 0.458
b5 F#-Gb 1.4375 389.230 45/32 380.769 1.4142 382.925 8.462 6.305 -2.156
4 F 1.3750 372.307 4/3 361.025 1.3348 361.433 11.282 10.874 -0.408
3 E 1.2500 338.461 5/4 338.461 1.2599 341.148 0.000 -2.686 -2.686
b3 D#-Eb 1.1875 321.538 6/5 324.923 1.1892 322.000 -3.385 -0.462 2.922
2 D 1.1250 304.615 9/8 304.615 1.1225 303.928 0.000 0.687 0.687
b2 C#-Db 1.0625 287.692 25/24 282.051 1.0595 286.870 5.641 0.822 -4.819
Root C 1.0000 270.769 1/1 270.769 1 270.769 0.000 0.000 0.000
more questions:
1. Do we have a definition for JI yet? 2. Are we free to change the ratio fractions in the given JI lists and still call it JI? 3. What is meant by "beatless"? 4. In "tune the beats out" do we mean ALL beats, or just certain ones? [This message was edited by ed packard on 24 September 2003 at 08:00 AM.]
b0b edited chart for formatting [This message was edited by b0b on 24 September 2003 at 04:03 PM.] |
Rick Aiello
Member From: Berryville, VA USA
|
 posted 24 September 2003 08:37 AM
profile
posted 24 September 2003 08:37 AM
profile
Since you asked ...  Just Intonation is a Key-Based system that uses fractions to define pitches. To differentiate between JI systems ... the tuning fractions are "restricted" to prime numbers up to a certain upper limit. EX: 3 Limit JI ... all fraction factors are multiples of 2 or 3 5 Limit JI ... all fraction factors are multiples of 2,3 or 5 7 Limit JI ... all fraction factors are multiples of 2,3,5 or 7 11 Limit JI ... all fraction factors are multiples of 2,3,5,7 or 11 13 Limit JI ... all fraction factors are multiples of 2,3,5,7,11 or 13 Here is a list of the various fractions associated with the JI systems for the chromatic scale ... Limits to JI The 5 Limit system seems to be the "best" for 12 tones ... The 3 Limit system doesn't handle thirds well .... The 7, 11 and 13 Limit systems offer lots of variety but some are quite "strange" to traditional ideas of harmony. As far as tuning guitars "beatless" ... the 5 limit system and the harmonic series "jive" very well ... particularly the first 5 harmonics (root, fifth, and third) ... which are the ones primarily used to get any open tuning beatless ... As you pointed out ... the sixths of the 5 limit JI system and the harmonic series don't agree ... But for a tuning like C6 ... it is more important to get the E and A beatless than it is to get the A to "agree" with the 13th harmonic of C. As far as what "beatless" means ... I approached the subject from several different angles in the thread by JD Sauser. [This message was edited by Rick Aiello on 24 September 2003 at 09:51 AM.]
|
Larry Bell
Member From: Englewood, Florida
|
 posted 24 September 2003 10:02 AM
profile
posted 24 September 2003 10:02 AM
profile
Rick,
That is an EXCELLENT summary. It reinforces stuff I've read in several different places and then explains the realities of it. The reference link is also very useful.------------------
Larry Bell - email: larry@larrybell.org - gigs - Home Page
2003 Fessenden S/D-12 8x8, 1969 Emmons S-12 6x6, 1971 Dobro, Standel and Peavey Amps
|
ed packard
Member From: Show Low AZ
|
 posted 24 September 2003 11:30 AM
profile
posted 24 September 2003 11:30 AM
profile
And there we have it folks, ..a reasonable, functional definition of JI, thanks to Rick and his Naval Post Grad school friend.In summation: To the extent that the above definition is accepted; JI is a "class" of tunings. Yes you can change the ratio fractions to get what you want (within limits) and still call it JI. Something is bound to beat somewhere, ..that which is not heard (inaudible) is of lesser consequence. JI is a "one key" thing on fixed string length instruments, but on the steel the key is moveable per bar position, the key is not moveable by choosing other intervals/strings as a scale root; Think PSG and compensators. Aside from JI: The harmonic content of a string is a function of string stiffness, taper, clamping method, roundness, core/winding relationships, and a few other items. The equations I used to get the h series do not consider the above issues. If one has an interest in such, an examination of literature/text books on side/end/edge/center clamped/hinged plates and membranes will be enlightening; Think drum heads, cymbals, bars as in Xylophones, gongs, suspended rods, and the like, ..each with their own harmonic content. |
Larry Bell
Member From: Englewood, Florida
|
 posted 24 September 2003 12:06 PM
profile
posted 24 September 2003 12:06 PM
profile
I don't really think of JI as 'one key' either. e.g., I have always tuned C# as the third of A rather than as the sixth of E. But I don't really tune beatless anyway.------------------
Larry Bell - email: larry@larrybell.org - gigs - Home Page
2003 Fessenden S/D-12 8x8, 1969 Emmons S-12 6x6, 1971 Dobro, Standel and Peavey Amps
[This message was edited by Larry Bell on 24 September 2003 at 12:07 PM.] |
Bobby Lee
Sysop From: Cloverdale, North California, USA
|
 posted 24 September 2003 04:25 PM
profile
posted 24 September 2003 04:25 PM
profile
quote:
I have always tuned C# as the third of A rather than as the sixth of E.
In the JI system, they are the same thing.A is E times 4/3 (the fourth).
C# is E times 5/3 (the sixth). But also, C# is A (the fourth of E) times 5/4 (the JI third).
C# = E x 4/3 x 5/4 = E x 20/12 = E x 5/3.
This is why I prefer fractions to decimals. They make it much easier to understand the relationships between the notes. Ed... In your chart above, the differences between the pitches would be much easier to understand in cents than in Hz.
My advice remains: Read Partch! ------------------
 Bobby Lee - email: quasar@b0b.com - gigs - CDs, Open Hearts Bobby Lee - email: quasar@b0b.com - gigs - CDs, Open Hearts
Sierra Session 12 (E9), Williams 400X (Emaj9, D6), Sierra Olympic 12 (C6add9),
Sierra Laptop 8 (D13), Fender Stringmaster (E13, A6),
Roland Handsonic, Line 6 Variax |
Bobby Lee
Sysop From: Cloverdale, North California, USA
|
 posted 24 September 2003 04:40 PM
profile
posted 24 September 2003 04:40 PM
profile
Another JI example:The second interval is 9/8.
The fourth interval is 4/3.
The fifth interval is 3/2. You can calculate the fifth from the fourth: 4/3 x 9/8 = 36/24 = 3/2 Proof that the interval between the fourth and the fifth is a JI second. |
ed packard
Member From: Show Low AZ
|
 posted 24 September 2003 05:25 PM
profile
posted 24 September 2003 05:25 PM
profile
b0b and others; If you like cents, then that is the way YOU should do it. If you like fractions, then that is the way YOU should do it.
Beats are in Hz.If you think that it would help anyone, feel free to to redo it in other terms.
To increment cents in ET, mult by 2^(1/1200)= 1.00058 if A =440, find A# =
To decrement cents in ET, mult by 1/(2^(1/1200)) 0.99942 440*(2^(1/12))=
To increment halftones in ET, mult by 2^(1/12)= 1.05946 466.1637615
To decrement cents in ET, mult by 1/(2^(1/12))= 0.94387
To increment/decrement by a number (n) of change (1/12) to (n/12) in the above equations. This leads to another possible thread, ..Tuning JI with an ET tuner, any volunteers?
[This message was edited by ed packard on 25 September 2003 at 06:44 AM.] [This message was edited by b0b on 25 September 2003 at 10:41 AM.] |
Hans Holzherr
Member From: Ostermundigen, Switzerland
|
 posted 25 September 2003 02:21 AM
profile
posted 25 September 2003 02:21 AM
profile
quote:
You can calculate the fifth from the fourth:4/3 x 9/8 = 36/24 = 3/2
Note that the JI cent numbers of intervals to be added can be added.
Example: A (a fourth up from E) is tuned to -2 cents. C# (a third [-14 cents] up from A) is tuned to -2-14 = -16 cents. Or, as in the quote, a fifth equals -2(fourth)+4(second) = +2 cents. This addition of cents corresponds to the multiplication of frequencies because cent numbers are actually logarithms. BTW, I have no problem to tune my F's to -29 cents. When pressing A-F I always position the bar a little bit higher than the fret indicates.
[This message was edited by Hans Holzherr on 25 September 2003 at 02:35 AM.] [This message was edited by Hans Holzherr on 25 September 2003 at 02:39 AM.] |
David Doggett
Member From: Philadelphia, Pennsylvania, USA
|
 posted 29 September 2003 10:30 AM
profile
posted 29 September 2003 10:30 AM
profile
Ed, sorry to take so long answering your question. I got a new computer and had to transfer my internet connection to it. In the chart I posted above comparing the JI and ET versions of the E scale, to get the cents for the intervals of the JI (5 limit) scale you multiply the log of the JI ratio by 1200/log 2, or:log(n/p) x 3986.3137 You can also look up these JI intervals in ratios or cents on the Anatomy of an Octave link posted by Rick. To convert the difference between ET and JI in cents to an A=440 Hz readout, I used the fact that, around 440, 1 Hz = 4 cents. It is difficult to hear a difference of less than 5 cents, so 1 Hz difference is imperceptible to most people (around 440). But 2 Hz is 8 cents, and that can be heard by anyone with a decent ear. I know, because that's how much the cabinet drop is on my Fessy.  | |

 The Steel Guitar Forum
The Steel Guitar Forum
 Pedal Steel
Pedal Steel
 JI tuning.. What is it?
JI tuning.. What is it?



 Bobby Lee - email:
Bobby Lee - email: 



